Pip Pixel Shader Dv2.1X – Displacement Feedback
This post focuses on non-linear video feedback.
Pip Pixel Shader Dv2.1X – Displacement Feedback
This post is a continuation of a previous post: Pip Pixel Shader Dv2.0X (! Link !)
This post focuses on the video feedback effect that is prevalent in this shader. Below are the inspiration for the effect, my twisted implementation, and some fun example loops.
Video 1: Twitter Promo 22Q3
Video Feedback – Inspiration
Dude837 / Sam has a “delicious Max Tutorial” on video “reverb”, where they explain a patch using an alpha-overlay and displacement shader . It’s worth a watch and a subscribe if you deal with MAX. After some testing, I had to incorporate this displacement feedback into this pixel shader in some form.
Video i-EXTERNAL (Ref): “Reverb” in MAX – Dude837 / Sam
Video Feedback – Implementation
Building on this framework, I replaced the td.rota.jxs transform shader (which has parameters like zoom, position, rotation) with a jit.gl.pix. This allows the use of vector math with imaginary numbers to create a new set of non-linear transformations to control the video feedback (fun fact, MAX has imaginary vector functions built in!) The exact vector “math” was arbitrary, mostly done by “guess-and-check”. For others interested in achieving similar effects, the behavior reminds me of jit.gl.bfg, which might be a more direct route for similar transformations.
Figure 1: Pip Shader Architecture
For context in the shader architecture, feedback is implemented between image matrices $A_1$ and $A_2$. (See the previous post (!!! link !!!) for more context)
Video 2: Fluid Noise #2
Fluidic Feedback Behavior
This is the fun section. I generally added some pixel noise before the feedback to better follow the direction of the feedback. The result: Much of the following videos have a fluid-like behavior, to the point that it’s eerie considering the lack of any fluid flow modeling.
Video 3: Fluid Noise #1
Video 4: Fluid Noise #3
Fluidic Feedback – Loose Math Ramplings: The feedback effect transforms the incoming image with an arbitrary complex equation (using imaginary numbers), pastes the transformed image on the canvas, and then repeats, transforming the image further along the complex equation. This is a bit reminiscent of a vector field in the sense that every X,Y point has a direction (or “slope”), except it is from a complex equation.
For those who don’t know imaginary math concepts, Wiki has some helpful examples for visualizing complex equations.
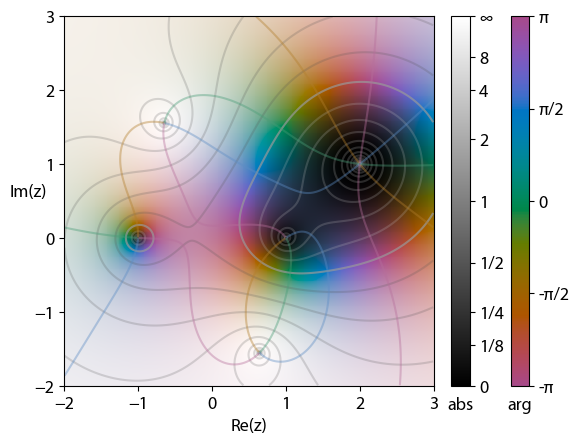Figure i-EXTERNAL (Ref): Color graph of the function f(x) = (x2 − 1)(x − 2 − i)2/x2 + 2 + 2i.
Many complex equations have local minimums (where points converge), and local maximums (where points diverge). As the image gets transformed according to the complex equation, it makes sense the image itself will start to converge towards the local minimums. However, the nature of displacement feedback means the image is constantly “perturbed” out of local minimums.
While not a mathematically robustly description, the effect is as if the image pixels carry a “momentum” of sorts, and can sling-shot around local minimums. As a grounded analogy, it’s like a classic coin vortex game, except the coin is a ball and there is wind blowing on the ball, and there are many balls.
Figure ii-EXTERNAL (Ref): Coin vortex game
GIF i-EXTERNAL (Ref): Computational Fluid Dynamics simulation of a sphere under unsteady occilating flow
Video 5: Data Smearing Wave
Video 6: Gritty Fluid Wave-to-Sphere
See Dv2.1X in action:
Video 7: 2021 Collab: A: M68K / V: PlasamPip
The files within this web page are licensed under a CC BY-NC-SA 4.0 Attribution-NonCommercial-ShareAlike International license.